衛星軌道を運動方程式を数値的に解く¶
はじめに¶
次の記事で解説されている、ニュートンの運動方程式を数値的に解くことで衛星軌道を計算することを習ってみます。
Pythonを使って人工衛星の軌道を表現する~軌道6要素、TLE~(宙畑)
この記事では、運動方程式に万有引力をさらっと記載して、すぐにPythonコード(常微分方程式を数値計算)に落としています。
しかし、なぜそうなるのかすぐに理解できなかったので、展開を考えながら追ってみました。
運動方程式をPythonで解く¶
運動方程式を衛星に適用¶
人工衛星はニュートンの運動方程式に従って飛行(運動)します。ニュートンの運動方程式は、次の式で表現されます。
$ m\boldsymbol{a} = \boldsymbol{F} $
- mは人工衛星の質量、 a は加速度、 F は人工衛星に作用する力で、太字はベクトル量を示します。
運動方程式の加速度を位置ベクトルで表現¶
主変数を、グラフにプロットしたい位置 r (x, y, z)とします。
加速度は、次の式で位置ベクトルで置き換えることができます。
$ \boldsymbol{a} = \dfrac{ d^2 \boldsymbol{r}}{dt^2} $
位置ベクトルで運動方程式を表現すると、次の式となります。
$ m \dfrac{ d^2 \boldsymbol{r}}{dt^2} = \boldsymbol{F} $
万有引力の大きさ¶
人工衛星に作用する力は、地球と人工衛星との2体間に働く万有引力です。地球の重心を原点として、地球重心と人工衛星重心との距離を r、地球の質量を M 、人工衛星の質量を m 、重力定数(万有引力定数)を G とすると、万有引力の法則から
$ F = G\dfrac{Mm}{r^2} $
と表せます。
- 大きさ(絶対値)を表わすので、F はベクトル量(太字)ではなくスカラー量で記載
- $ G = 6.67430(15) \times 10^{-11} [Nm^2/kg^2] $
CODATA 2022より(国際学術会議 ISC のデータに関する委員会で4年ごとに物理定数について最新の改定値を公開)。(15)は標準不確かさで $ 0.00015 \times 10^{-11} $ となる。 $ 単位 N は kg・m/s^2 $ で表されるので、万有引力定数の単位は、$ m^3/kg・s^2 $ となる。 - $ M = 5.972 \times 10^{24} [kg] $
理科年表より
補足
- 地球赤道半径は、GRS80準拠楕円体の長半径より、6378.137 km
- 地球局半径は、GRS準拠楕円体の長半径(上述)と扁平率 1/298.257222101 より、6356.752 km (長半径 * (1-扁平率))
人工衛星に作用する力(ベクトル量)¶
万有引力による人工衛星に作用する力のベクトル量 F は、原点(地球)向きに働くので、衛星の位置ベクトル量 r を用いると、
万有引力の式に $ - \frac{\boldsymbol{r}}{|r|} $ をかけた次の式になると思います。
$ \boldsymbol{F} = -G\dfrac{Mm}{r^2} \dfrac{\boldsymbol{r}}{|r|} $ $ = -G\dfrac{Mm}{r^3}\boldsymbol{r} $
運動方程式を1階常微分方程式で表現¶
記事では、Pythonのライブラリ SciPy のodeintライブラリ を使って運動方程式を数値的に解いています。
上述の運動方程式は、変数 r の2階常微分方程式なので、ライブラリを利用して数値解を得るために階数を1階にするため、従属変数 v を導入して2元連立1階微分方程式を立てて解いています。
$ \dfrac{d\boldsymbol{r}}{dt} = \boldsymbol{v} $
$ \dfrac{d\boldsymbol{v}}{dt} = - \dfrac{GM}{r^3} \boldsymbol{r} $
- 前者は、位置 r の1階微分が速度 v となる式
- 後者は、万有引力で表現した運動方程式 $ m\boldsymbol{a} = -\dfrac{GMm}{r^3}\boldsymbol{r} $ の両辺に登場する m を割った残りの式で、加速度 a を速度の微分に置き換えた式
連立式で、 r を(x,y,z)、 v を(vx,vy,vz)とし、左辺の微分項を、漸化式のn+1で表すと
\begin{eqnarray}
\left\{
\begin{array}{l}
x_{n+1} = vx_n \\
y_{n+1} = vy_n \\
z_{n+1} = vz_n \\
vx_{n+1} = -\dfrac{GM}{r^3} x_n \\
vy_{n+1} = -\dfrac{GM}{r^3} y_n \\
vz_{n+1} = -\dfrac{GM}{r^3} z_n
\end{array}
\right.
\end{eqnarray}
Pythonで数値的に解く¶
SciPyのodeintを使って常微分方程式を数値的に解きます。
利用するライブラリ¶
ベクトルや数値生成などを行う numpy ライブラリ、微分方程式を解く scipy ライブラリ(の中のodeintライブラリ)、グラフをプロットして表示する matplotlib ライブラリ(の中のpyplotライブラリ)をimportします。
import numpy as np # 数値計算ライブラリ
from scipy.integrate import odeint # 常微分方程式を解くライブラリ
import matplotlib.pyplot as plt # グラフ描画ライブラリ
- odeintは、Ordinary Differential Equation の略
微分方程式を漸化式で表現¶
微分方程式を、前の時刻の解から次の時刻の解を求める漸化式で表現(離散化)します。
odeintでは、前の時刻の解と時刻を引数として入力し、次の時刻の解を戻り値として返却する関数として定義します。
# 二体問題の運動方程式
def func(x, t):
GM = 398600.4354360959 # 地心重力定数
r = np.linalg.norm(x[0:3])
dxdt = [x[3],
x[4],
x[5],
-GM * x[0] / (r**3),
-GM * x[1] / (r**3),
-GM * x[2] / (r**3)]
return dxdt
入力のxは、前の時刻における衛星の位置・速度で[x, y, z, vx, vy, yz] の6つのベクトル(配列)です。
戻り値は、前の時刻の値から算出した今の時刻の衛星の位置・速度です。np.linalg.norm 関数は、ベクトルの大きさ(2-ノルム)を計算します。
戻り値の前半の3つは、$ \frac{d\boldsymbol{r}}{dt} = \boldsymbol{v} $ の右辺値の計算結果に対応し、ここでは速度 v が結果となるので、入力xのvx, vy, vzをそのまま入れます。
戻り値の後半の3つは、$ \frac{d\boldsymbol{v}}{dt} = -G\frac{M}{r^3} \boldsymbol{r} $ の右辺値の計算結果に対応し、入力xのx,y,zから計算した結果を入れます。
初期値を定義し微分方程式を解く¶
# 微分方程式の初期条件
x0 = [10000, 0, 0, 0, 7, 0] # 位置(x,y,z) + 速度(vx, vy, yz)
t = np.linspace(0, 86400, 1000) # 1日分の軌道伝播
# 微分方程式の数値計算
sol = odeint(func, x0, t)
初期位置 (10000, 0, 0)、初期速度 (0, 7, 0) としています。
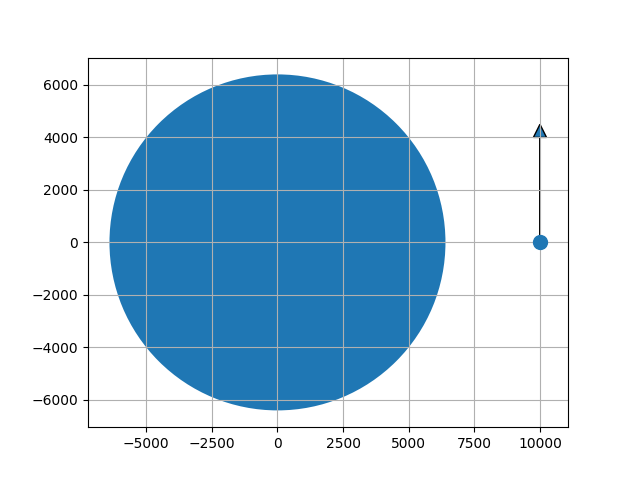
上の図は、3次元座標のうち(X, Y)をプロットするものです。人工衛星の初期位置(x,y,z) を、(10000, 0, 0)としました。この位置で、地球を左回りに周回するための速度はY方向に正の成分を持つ必要があるので、人工衛星の初期速度(vx, vy, vz)を、(0, 7, 0)としています。
時刻は、開始=0、終了=86400で、1000個の時刻データを生成しています。
odeint関数に、微分方程式の漸化式を定義した関数と、初期状態、時刻を渡します。
odeint関数の戻り値は、時刻とその時刻の各状態の配列で、$ [[t_i], [x_i, y_i, z_i, vx_i, vy_i, vz_i]] $ となっています。
微分方程式の数値解のプロット¶
グラフに数値解のx,y平面のプロットをします。
plt.plot(sol[:, 0], sol[:, 1], 'r')
plt.grid() # 格子を描く
plt.gca().set_aspect('equal')
plt.show()
matplotlibのpyplotライブラリの関数plotに、x軸、y軸の数値列を指定、プロットの色と種類に'r' (赤色を指定、形状はデフォルトのsolid line)を指定しています。
横軸は、すべての時刻における状態の1つ目の値(sol[:, 0])、縦軸は、すべての時刻における状態の2つ目の値(sol[:, 1])です。
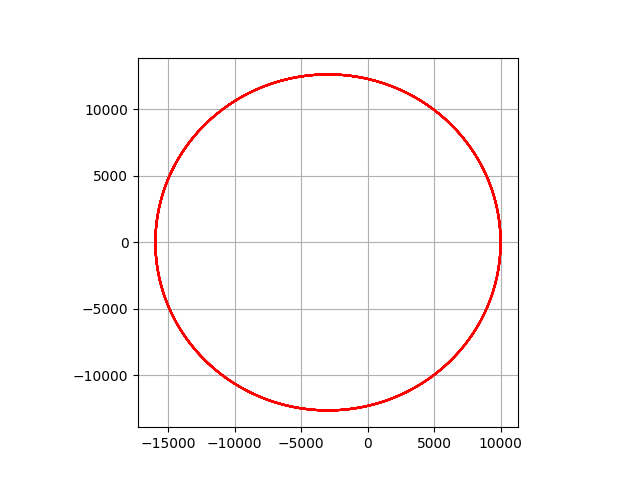
このプログラムは次です。
地球のプロット¶
グラフに、地球を円として描画します。
matplotlibには、大きく分けて2種類のインタフェース(API)があります。
- pyplotインタフェース
- axインタフェース
前者は、matplotlibライブラリの基となった MATLAB に近いインタフェースです。後者は、Pythonにおけるオブジェクト指向インタフェースです。
グラフ描画の細かな調整をするにはオブジェクト指向インタフェースが必要になるので、最初からaxインタフェースを理解するのがよいようです。
ですが、簡便のため今回は 前者のインタフェースで地球を描画します。
earth = plt.Circle((0, 0), 6400)
plt.gca().add_patch(earth)
plt.Circle関数で、中心を(0,0)、半径を6400とした円を作成します。plt.Circleは、実際にはmatplotlib.patches.Circleへの
plt.gca()関数で現在描画対象のAxisを取得し、add_patch関数でそこに図形を貼ります。
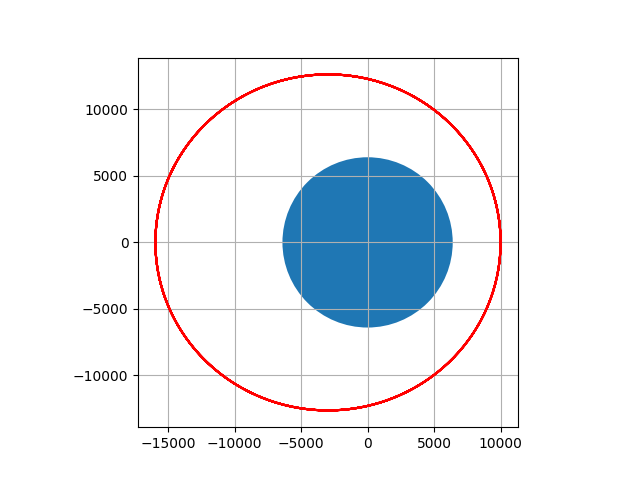
add_patch関数と同様の機能を持つadd_artist関数もあります。add_artist関数で貼った図形は、グラフの自動スケール対象外となります。
このプログラムは次です。3次元プロット¶
せっかくなので、3次元グラフに軌道と地球をプロットしてみます。Matplotlibライブラリで3次元グラフにプロットする場合、MATLAB風インタフェースではなく、オブジェクト指向インタフェースを使います。
衛星軌道の3次元プロット¶
まず、3次元グラフを用意します。Figureオブジェクトを取得し、projectionパラメータに '3d'を指定してプロットするグラフを用意します。
用意したグラフは Axesオブジェクトを通じてプロットしていきます。
fig = plt.figure()
ax = fig.add_subplot(projection='3d')
次に、Axesオブジェクトに対して3次元データをプロットします。
プロット後、3つの軸についてアスペクト比を等しく(1:1:1)します。
ax.plot(sol[:, 0], sol[:, 1], sol[:, 2], 'b')
ax.set_aspect('equal')
plt.show()
実行結果は次となります。
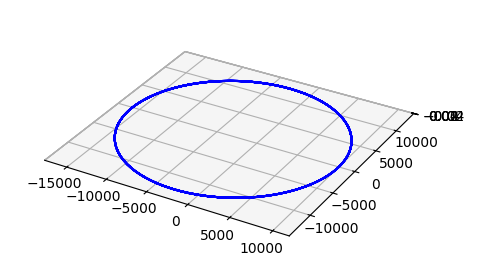
初期速度のZ軸成分がゼロなので、軌道は常にz=0となり、せっかく3Dプロット機能を使っているのにプロット結果が2次元平面になっています。
そこで、初期速度のZ軸成分に値を持たせます。
- x0 = [10000, 0, 0, 0, 7, 0] # 位置 (x,y,z) と 速度 (vx, vy, vz)
+ x0 = [10000, 0, 0, 0, 6, 3.6] # 位置 (x,y,z) と 速度 (vx, vy, vz)
実行結果は次となります。
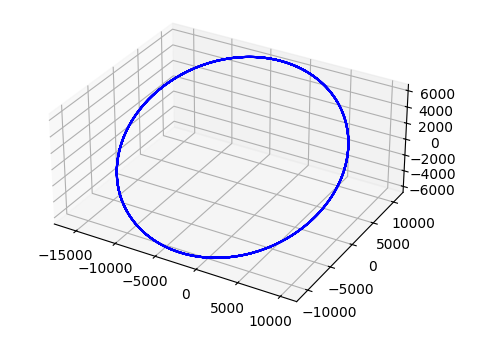
このコードは
地球の3Dプロット¶
地球を原点を中心に、半径を6400とした真球のワイヤフレームを3Dプロットします。
球面上の点をグリッド状に生成します。
球面上の点の座標は、球の中心が原点の場合、極座標系で2つの偏角 $\theta, \phi$ を用いて次の式で算出します。
$$
\left\{
\begin{align}
x &= r \times \sin(\theta) \cos(\phi) \\
y &= r \times \sin(\theta) \sin(\phi) \\
z &= r \times \sin(\theta)
\end{align}
\right.
$$
- r: 球の半径
- $0 \leq \theta \leq \pi$
- $0 \leq \phi \leq 2\pi$
この数式をPythonコードで表現します。
まず、球の表面上の点群を生成する関数を定義します。
def sphere(radius):
theta, phi = np.mgrid[0: np.pi:50j, 0: 2 * np.pi:100j]
x = radius * np.sin(theta) * np.cos(phi)
y = radius * np.sin(theta) * np.sin(phi)
z = radius * np.cos(theta)
return x, y, z
Matplotlib の3D Axesオブジェクトのplot_wireframe で球面上の点群を渡すと、ワイヤフレームがプロットできます。
x, y, z = sphere(6400)
ax.plot_wireframe(x, y, z, linewidth=0.2)
軌道と地球のプロット結果¶
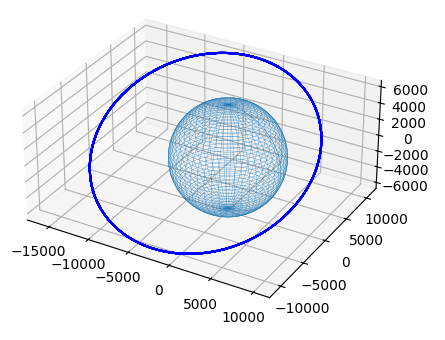
このコードは
Pythonの書き方メモ¶
ライブラリの利用¶
このプログラムでは、次の3つの外部ライブラリを使用しています。
- NumPy
- SciPy
- Matplotlib
NumPyライブラリは、配列機能、様々な数学計算機能を提供します。
SciPyライブラリは、高度な科学技術計算、例えば微積分などを提供します。
Matplotlibライブラリは、さまざまなグラフのプロット機能を提供します。
パッケージのインポート¶
NumPyライブラリは、numpyパッケージ一つをimportすると利用できます。次のように エイリアス名 np でimportすることでコード記述を短くできるようにするのが慣例です。
import numpy as np
SciPyライブラリは、scipyパッケージの下にたくさんのサブパッケージを持つ構成となっています。
ここでは、scipyパッケージ下のintegrateサブパッケージをfromで指定し、コード中で使用するodeint関数をimportします。コード中でパッケージ・モジュール
from scipy.integrate import odeint
Matplotlibは、グラフを書くためのライブラリで、折れ線グラフ、棒グラフ、ヒストグラム、散布図、3Dプロットなどを作成します。
Matplotlibライブラリを利用するためインタフェースが収められたpyplotパッケージをエイリアス名 plt でimportします。
import matplotlib.pyplot as plt
importと、from ... import の違い¶
import A とすると、A(パッケージまたはモジュール)をインポートし、インポートした名前(例、A)を起点にそのパッケージまたはモジュールに定義される公開インタフェースを呼び出すことができます。例えば、A.funcA、A.funcB などです。
一方、from A import B とすると、Bだけを呼び出すことができます。直接 B と記述することができますが、B以外の公開インタフェースを呼ぶことはできません。
関数の定義¶
pythonは、関数を定義する際、defキーワードに続けて関数名と括弧の中に引数を記述します。末尾にコロンを記載します。 def 関数名(引数名, ...):
関数の中身は、関数定義行の次の行から1レベルのインデントをして記述します。
関数の終わりは、関数定義行と同じインデントのコードの直前までとなります。
def myfunc(arg1, arg2): # 関数の定義
sum = arg1 + arg2
return sum
print('abc') # 関数の定義の外
変数の定義¶
変数名を左辺に、= で右辺に式(リテラルや、計算式、関数の戻り値など)を記載します。
リスト(配列)¶
Pythonは、厳密には配列がないのでリストを使います。リストの初期化は、大括弧で囲った中に値をカンマ区切りで記述します。
x0 = [7000, 0, 0, 0, 7, 0]
リストの個々の要素のアクセスは、x0[3] のように変数名に大括弧で取り出す要素のインデックスを番号(0で開始される順番を示す)で指定します。
リストから複数の要素を取り出す場合、x0[0:3] のようにコロンを使ったスライスと呼ぶ記法で指定します。この例では、インデックス0から2(コロンの後の3はインデックス3よりも前を示す)の要素をリストで取り出します。[x[0],x[1],[x2]] と等価です。
Numpyライブラリの関数¶
ベクトルのノルム¶
ベクトルの大きさ(2-ノルム:ユークリッドノルム)を計算する関数が Numpyに用意されています。
引数に、リスト(ベクトルの要素のリスト)を入れると、ベクトルの大きさ(要素の二乗和の平方根)を返却します。
r = np.linalg.norm(x[0:3])
等間隔の数列¶
1,3,5,7,... のような等間隔の数列(等差数列)を生成する関数が Numpy に用意されています。
引数に、最初の値、最後の値、数列の要素数を指定すると、数列をリストで返却します。
t = np.linspace(0, 86400, 1000) # 1日分の軌道伝播 1000の区分で計算
上のコードは、0から86400までの1000個の要素の数列を生成します。
グリッド(格子点)を生成¶
2つの軸(θとφ)のグリッド(格子点)を等間隔に生成する mgrid 関数を使用します。
θの値を、0からπ、φの値を0から2πまで、それぞれ50点、100点を生成し、これを組み合わせ(かけ合わせ)ることでθとφの格子点を50×100の5000点を生成します。
theta, phi = np.mgrid[0:np.pi:50j, 0:2*np.pi:100j]
2次元の格子点を生成する、50行100列の行列を2つ生成します。0:np.pi:50jは、コロンで区切った3つの値を指定しており、始点、終了点(含まない)、増分(jが付かない値指定の場合)または始点と終点の間に幾つの点を生成するかの区分数(jをつけた値指定の場合)となります。
thetaは、0からπの間を50個に分割した各点の値を行方向に50個、列方向は同じ点の値を100個並べた50行100列の2次元配列になります。
[[0, 0, 0, ..., 0], [0.064, 0.064, 0.064, ..., 0.064], [0.128, 0.128, 0.128, ..., 0.128], ..., [3.141, 3.141, 3.141, ..., 3.141]]
phiは、0から2πの間を100個に分割した各点の値を列方向に100個、行方向は同じ点の値を50個並べた50行100列の2次元配列になります。
[[0, 0.064, 0.127, ..., 6.220, 6.283], [0, 0.064, 0.127, ..., 6.220, 6.283], [0, 0.064, 0.127, ..., 6.220, 6.283], ... [0, 0.064, 0.127, ..., 6.220, 6.283]]
thetaとphiをかけると、θとφのグリッド(格子点)が生成できます。
mgridによる格子点生成のイメージ¶
xの値を(2,4,6)、yの値を(1,3,5,7)とする格子点を生成します。mgrid関数は、xとyの方向が下表のように、xが行方向、yが列方向となります。
| Y | |||||
| 1 | 3 | 5 | 7 | ||
| X | 2 | (2,1) | (2,3) | (2,5) | (2,7) |
| 4 | (4,1) | (4,3) | (4,5) | (4,7) | |
| 6 | (6,1) | (6,3) | (6,5) | (6,7) | |
上述の格子点の座標から、Xだけ取り出したもの、Yだけ取り出したものは次となります。
| Xだけ取り出し | Yだけ取り出し |
\begin{bmatrix} 2 & 2 & 2 & 2 \\ 4 & 4 & 4 & 4 \\ 6 & 6 & 6 & 6 \end{bmatrix} |
\begin{bmatrix} 1 & 3 & 5 & 7 \\ 1 & 3 & 5 & 7 \\ 1 & 3 & 5 & 7 \end{bmatrix} |
これを、NumPyのmgrid関数で表現すると、次のようになります。
x, y = np.mgrid[2:8:2, 1:8:2]
2:8:2は、2を開始点、8を終点、増分を2と指定するので、(2,4,6)となる1:8:2は、1を開始点、8を終点、増分を2と指定するので、(1,3,5,7)となる
このx,yを、例えば Matplotlibのplot関数に渡すと、格子点がプロットできます。
参考までに、mgrid関数と似た機能を持つmeshgrid関数がありますが、meshgrid関数が生成する行列は、xが列方向、yが行方向とmgrid関数が生成する行列から転置したものになります。
常微分方程式¶
SciPyライブラリには、常微分方程式の数値解を求める機能が複数提供されています。今回は、odeintを使います。
odeintは、FORTRANのodepackライブラリのLSODAアルゴリズム(問題に応じてRunge-Kutta法とBDF法を切り替えて計算)を使って常微分方程式の数値解を算出します。
微分方程式の逐次計算の関数(ここでは func)、初期状態(ここではx0)、逐次のステップ(ここではt)を引数に与えると、逐次の値(ここでは区分された時刻)毎の状態を計算して返却します。
sol = odeint(func, x0, t)
返却された状態は、2次元配列の様式になっており、時刻tiにおける状態ベクトル(xi,yi,zi,vxi, vyi, vzi)となります。
軌道のプロット¶
Matplotlibライブラリを利用して、X-Yの2次元平面に軌道をプロットします。
ライブラリのAPIには、matlabインタフェースとオブジェクト指向インタフェースと大きく2種類が用意されています。今回は、簡潔のためmatlabインタフェースのみ使用します。
plot¶
plot関数の引数に、X座標のリスト、Y座標のリスト、プロットする形状を指定すると、折れ線グラフを表示します。グラフの各軸の範囲はプロットするデータに応じて自動的に変化します。
plt.plot(sol[:, 0], sol[:, 1], 'b')
横軸には、odeintの解のうち、位置のx座標を、縦軸にはodeintの解のうち、位置のy座標を、色を青でプロットします。
grid¶
plt.grid()
グラフに格子を表示します。
set_aspect¶
plt.gca().set_aspect('equal')
グラフの縦横比を1:1とします。
show¶
グラフを描画します。
微分方程式¶
なんとなく学生時代に数学でやったことがあるなぁ、くらいの知識では厳しいので、補足知識を得ることとします。
分類¶
微分方程式にはいくつかの分類があります。
- 常微分か、偏微分か
一変数関数(例:$ y = f(x) $)の微分は常微分方程式、多変数関数(例:$ y = u(x,y) $) の微分は偏微分方程式に分類されますニュートンの運動方程式は常微分方程式です。 - 線形か非線形か
微分項同士の掛け算がなければ線形(例 $ \frac{dy}{dx}、\frac{d^2y}{dx^2} $)、微分項同士の掛け算があると非線形(例 $ (\frac{dy}{dx})^2 $)に分類されます。多くの問題は線形微分方程式で表されます。 - 斉次か非斉次か
微分項に係る係数が定数であれば斉次、関数であれば非斉次になるようです。
斉次の例 $ a_1 \frac{dx}{dt} + a_0x = 0 $
非斉次の例 $ a_1 \frac{dx}{dt} + a_0x = f(t) $ → 両辺を $ f(t) $ で割ると、微分項の係数が $ \frac{a_1}{f(t)} $ のようにtの関数となります。 - 階数
微分している回数を項の階数と呼び、最も大きい階数がその微分方程式の階数となります。$ \frac{d^2x}{dt^2} $ は2階となります。
微分方程式¶
一般的に、一階常微分方程式は次の式で表現されます。
$ \frac{dy}{dx} = f(x, y) $
左辺の微分項と右辺の関数の双方に x, y が登場して混乱してしまいがちのため、理解促進のために少し冗長に表現すると
$ \frac{d}{dx}y(x) = f(y(x), x) $
微分方程式の数値解¶
微分方程式を数値的に解くには、オイラー法やルンゲクッタ法などがあり、変数を離散化して初期値から漸進的に計算していくことで解を得ます。
これらの方法で解ける微分方程式は、1階の線形斉次の常微分方程式です。
微分方程式を満たす解は無数にあるので、初期値を1点定めることで1つの解が得られます。
Python では、SciPyライブラリに常微分方程式の数値解を計算する関数がいくつか含まれています。
参考文献 ¶