One-Class SVM¶
概要¶
参考文献1 p.93より
手持ちの正常データを囲むような境界として、異常データと分離するような最小の球を1つ構成する手法です。この方法は、機械学習でよく知られるサポートベクターマシン(Support Vector Machine, SVM)を異常検知に応用したものです。
サンプルコードについて¶
Python 3.12をベースに記述します。また、型ヒントをなるべく記述しています。
文献1 のサンプルコードを試す¶
文献1の第5章と第7章に、One-Class SVMを使った異常検知のサンプルが掲載されています。
これをじっくり咀嚼しながらコードを書いていきます。
第5章は、平均と標準偏差を指定して乱数でデータを生成し、そのデータをOne-Class SVMで学習させ、その境界を表示するサンプルです。
第7章は、ワインの化学成分をまとめたデータを学習し、境界の表示(2変数版)または異常度のヒストグラムを表示するサンプルです。
第5章のサンプル¶
使用するライブラリの取り込み¶
import matplotlib.pyplot as plt
import matplotlib_fontja
import numpy as np
import pandas as pd
from pandas import DataFrame
from sklearn.svm import OneClassSVM
グラフにプロットするため、matplotlib.pyplotと、グラフに日本語を表示するため matplotlib_fontja を取り込みます。書籍のサンプルコードでは、グラフへの日本語表示に japanize_matplotlibを使用していますが、これは Python 3.12以降に対応していないので変更しています。
数学計算のためのnumpyライブラリ、データ分析のpandasライブラリ、機械学習ライブラリからOneClassSVMを取り込みます。
データの作成¶
# 生成するデータ数
N_DATA: int = 200
def generate_data(num: int) -> DataFrame:
""" 引数で指定した次元の乱数を2つ生成、DataFrameのx列とy列に設定し返却する """
df = pd.DataFrame()
np.random.seed(seed=0) # 乱数生成列を固定
df["x"] = 10.0 * np.random.randn(num) + 50 # num次元の乱数(平均50, 分散10)を生成
df["y"] = 10.0 * np.random.randn(num) + 50
return df
データを生成するgenerate_data関数を定義します。引数で指定した数をサイズとする x と y の列データを乱数で生成し返却します。
np.random.seedで固定値をセットすることで、以降の乱数生成列が毎回同じになります。動作確認に乱数要素を排除するときに有用です。
np.random.randnは、引数を1つ指定した場合は、指定した次元数のベクトル(配列で表現すると、1次元配列で要素数が引数)を乱数で生成します。
data: DataFrame = generate_data(N_DATA)
上で定義した関数を呼び出してデータを生成します。
xx, yy = np.meshgrid(np.linspace(0, 100, 1000), np.linspace(0, 100, 1000))
0から100の間を1000個で刻む格子点を生成するための行列を2つ生成します。行列xxとyyを組み合わせると格子点となります。
xxは、
$ \begin{bmatrix} 0 & 1 & 2 & \ldots & 100 \\ 0 & 1 & 2 & \ldots & 100 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 1 & 2 & \ldots & 100 \end{bmatrix} $
yyは、
$ \begin{bmatrix} 0 & 0 & \ldots & 0 \\ 1 & 1 & \ldots & 1 \\ \vdots & \vdots & \ddots & \vdots \\ 100 & 100 & \ldots & 100 \end{bmatrix} $
xxとyyの要素同士を組み合わせると、(0, 0), (1, 0), (2, 0) ... (0, 1), (1, 1), (2, 1) ... と格子点の座標が生成可能です。
3つのグラフ領域を準備¶
matplotlibライブラリを使用して、図(画像)にプロット領域を用意します。今回は3つのグラフを横並びに配置します。
fig = plt.figure(figsize=(16, 4.5))
fig.subplots_adjust(hspace=0.4, wspace=0.2)
ax1 = fig.add_subplot(131)
ax2 = fig.add_subplot(132)
ax3 = fig.add_subplot(133)
figure で引数figsizeに指定した大きさの画像を生成します。subplots_adjust で画像上でグラフの間隔(縦・横の余白)を指定します。add_subplot で画像上のグラフの縦横配置数と配置場所を指定し、そこにグラフを追加し、そのグラフに対する操作をするためのAxesオブジェクトを受け取ります。引数に指定する3桁のコードとグラフの配置は次のとおりです。
| 131 | 132 | 133 |
One-Class SVMに学習させる(左の図用)¶
# 左の図
clf = OneClassSVM(nu=0.05, kernel="rbf", gamma=0.0001)
clf.fit(data[["x", "y"]])
pred = clf.predict(data[["x", "y"]])
score = clf.decision_function(data[["x", "y"]])
OneClassSVMクラス¶
One-Class SVMの学習器を、ハイパーパラメータを指定して生成します。ハイパーパラメータは次の3種類があります。
- $ \nu $ (nu)
- カーネル関数
- $ \gamma $ (gamma)
One-Class SVMは教師なし学習で、正常データのみを学習し、外れ値を検出することで異常を検知をします。このとき、閾値として誤検出(偽陽性)をする割合を $ \nu $ (nu)で指定します。誤検出を0とすることは難しくフェールセーフの考え方として異常を正常と判断してしまう偽陰性は避けるため、ある程度の誤検出を許容するようにします。0.01を指定すると、100件のデータのうち1件は誤検出(正常データを異常として検知)することを許容することになるかと思います。あまり大きくすると頻繁に誤検出が起きてオオカミ少年になりますし、あまり小さいと判定境界が広がり外れ値を正常とみなしてしまいます。いくつかの文献を見た限りでは、0.05あたりがよく採用されているようです。
カーネル関数は、元のデータを高次空間にマッピングし正常データが原点から遠くの局所的に集まるように写像して、境界を高次空間における超球面で定義します。この球面は元のデータの次元において非線形な境界となります。(様々な記事を見ると球面という説明のほかに高次空間での平面(超平面)という説明もあり、どちらが正しいのか漫然としています)
一般的には radial basis functionを使用します。
- $ \gamma $ (gamma)は、カーネル関数の選択によって登場するパラメータです。RBFの場合次の式で使われます。
- $ \kappa(\boldsymbol{x},\boldsymbol{x'})=\exp(-\gamma |\boldsymbol{x} - \boldsymbol{x'}|^2) $
RBFは、0から1までの値を取り、2つのサンプル $ \boldsymbol{x}と\boldsymbol{x'} $ の間の距離が近いほどサンプルの類似度が高い(1に近い)となります。
境界の設定¶
fitメソッドで、引数に与えたデータを正常データとしてそれらを囲む境界(soft boundary)を定めます。
予測¶
predictメソッドで、引数に与えたデータが正常か否かを予測します。戻り値は、引数の各データに対応する予測結果のリスト(配列)で、1が正常、-1が異常を示します。
スコアの取得¶
decision_functionメソッドで、引数に与えたデータを正常・異常判断するためのスコアを返します。スコアはそれぞれのデータと境界との距離(マージン?)を返します。正の値は正常、負の値は異常、0付近は境界を示します。
格子点の外れ値判定¶
Z = clf.decision_function(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
ravel関数は、多次元配列を1次元配列にします。xxとyyはそれぞれ 1000x1000の2次元配列なので、ravel関数により 要素数が 100万個の1次元配列となります。
xx.ravel()は、[0, 1, 2, ... 100, 0, 1, 2, ... 100, 0, 1, 2, ..., 0, 1, ...]を返し、
yy.ravel()は、[0, 0, 0, ... 0, 1, 1, 1, ... 1, 2, 2, 2, ..., 100, 100, ...]を返します。
c_関数は、同じサイズの1次元配列を2つ指定すると、 [[0,0], [1,0], [2,0], ... [100,0], [0,1], [1,1], [2,1] ... [100,1], [0,2], [1,2], [2,2], ...[100,2],...[0,100], [1,100],...[100,100]]
と結合され、100万個の格子点が生成されます。
それぞれの格子点におけるOne-Class SVMの予測値スコア(その点と境界との間のマージン)をdecision_functionメソッドで取得し、xxやyyと同じ1000x1000の配列に変形します。
プロット¶
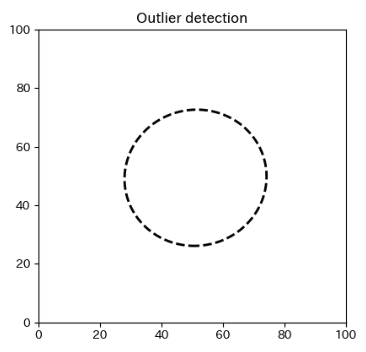
ax1.set_title("Outlier detection")
a = ax1.contour(xx, yy, Z, levels=[0], linewidths=2, colors="black", linestyles="--")
set_titleメソッドで左の図のグラフに題名をつけます。
contourメソッドで、格子点のx座標、y座標、各点の高さを指定、等高線は配列で指定すると配列の各値の高さで線を引きます。[0]と指定すると高さが0の1本の等高線となります。線幅2、色は黒、線種は破線で描きます。
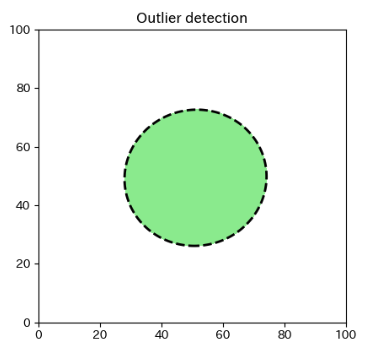
ax1.contourf(xx, yy, Z, levels=[0, Z.max()], colors="lightgreen")
contourfメソッドは等高線の線の間に色を塗ります。levelsで指定した 0と最大値の間を塗っています。
ax1.set_xlabel(r"$x_1$")
ax1.set_ylabel(r"$x_2$")
グラフのX軸、Y軸にラベルを設定します。上付文字、下付文字はLaTeX形式で記述することが可能で、$で囲って記述します。
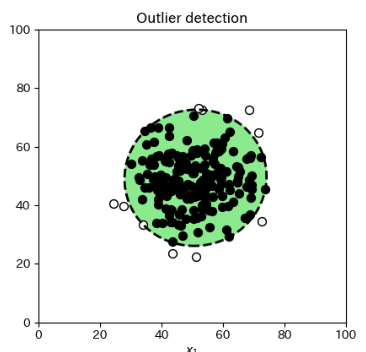
ax1.scatter(data["x"].iloc[np.where(pred>0)], data["y"].iloc[np.where(pred>0)], c="black", edgecolors="black", s=50)
ax1.scatter(data["x"].iloc[np.where(pred<0)], data["y"].iloc[np.where(pred<0)], c="white", edgecolors="black", s=50)
正常値を、黒塗りの丸で、異常値を白塗りの丸でプロットします。
予測値(predictメソッドの戻り値)の配列のなかから0より大きい値のある要素のインデックス群を np.where(pred > 0) で取り出し、ilocでインデックスが指す値を散布図に正常値として黒塗りつぶしでプロットします。
予測値の配列のなかから0より小さい値である要素のインデックス群を np.where(pred < 0) で取り出し、ilocでインデックスが指す値を散布図に異常値として白塗りつぶしでプロットします。
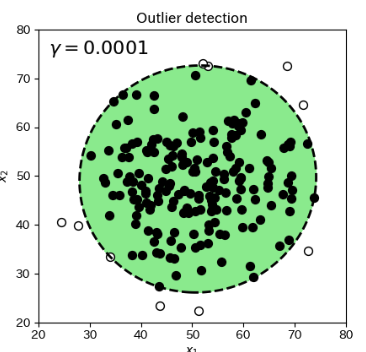
ax1.set_xlim(20, 80)
ax1.set_ylim(20, 80)
ax1.annotate(r"$\gamma=0.0001$", xy=(22,75), size=16, color="black")
x軸とy軸の表示範囲を20から80に設定、グラフ上に文字列を設定します。
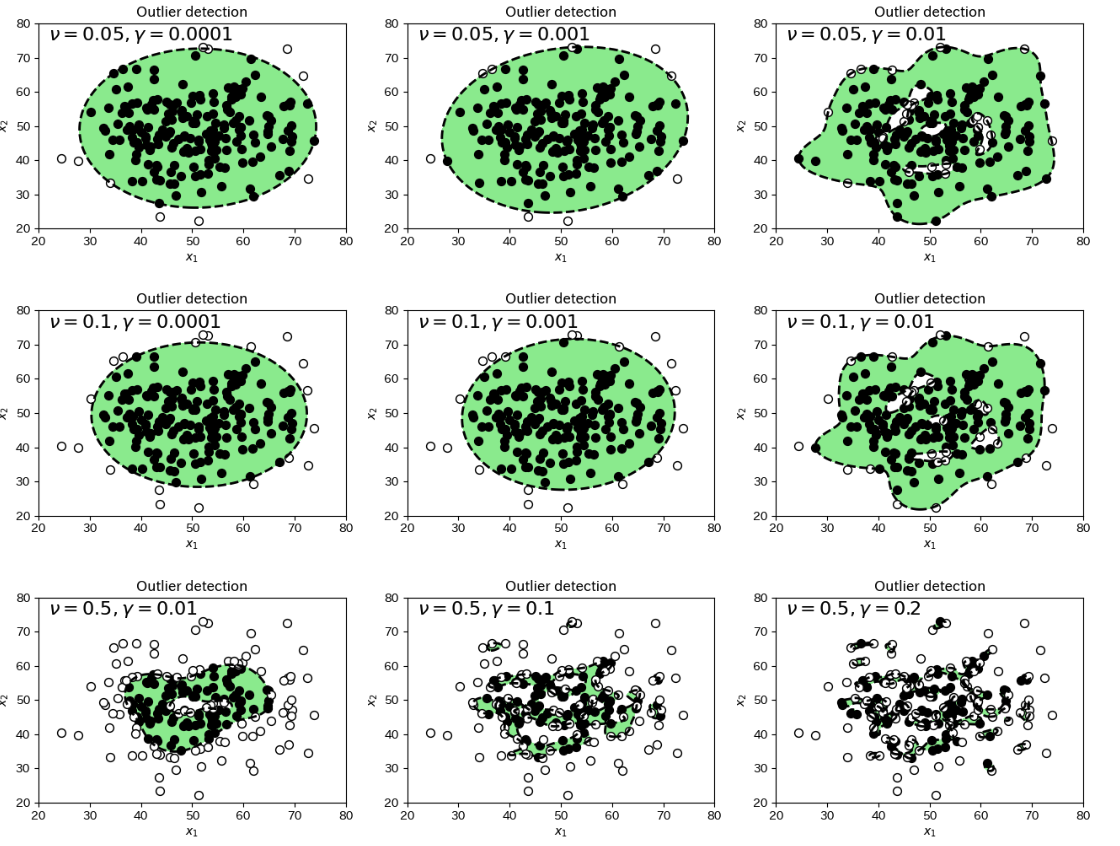
νとγのバリエーション9種¶
このプログラムをちょっと改修して、νとγの値の組み合わせを9種類変化してのプロットを作成しました。
第7章のサンプル¶
使用するライブラリの取り込み¶
import matplotlib.pyplot as plt
import pandas as pd
import scipy.stats as stats
from sklearn import svm
参考文献¶
1 書籍「Pythonではじめる異常検知入門-基礎から実践まで-」(江崎 剛史、李 鍾賛 著、笛田 薫 監修、科学情報出版 刊 2023年)
2 ブログ「『Pythonではじめる異常検知入門』を寄り道写経 ~ 第5章『入出力の情報に基づくアプローチ』 One-Class SVM」